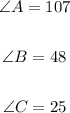Step-by-step explanation:
Given;
We are given the following information for a triangle;
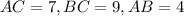
Required;
We are required to find the measures of angles A, B and C.
Step-by-step solution;
For any triangle with three sides given/available we can apply the cosine rule to calculate the missing angle(s).
The cosine rule is quoted below;
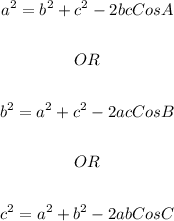
We shall now take angle A to begin with;
We start by making Cos A the subject of the equation;

With the refined form of the cosine formula we can now substitute and solve as follows;
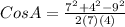
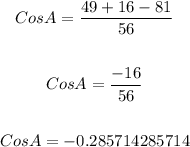
We can now use a calculator to find the value of arccos -0.2857...
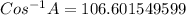
Rounded to the nearest degree the angle measure is;
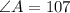
To solve for angle B, we can now apply the sine rule, since we have two sides and one of the angles. The sine rule is quoted below;
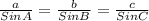
We have angle A, and side length a. We have side length b, which means we can solve for angle B. This is shown below;
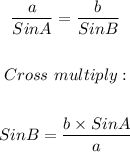
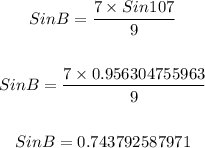
We can now use a calculator and find the arcsin of the decimal 0.7437...
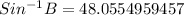
Rounded to the nearest degree, we now have;
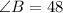
Note that the sum of angles in a triangle all sum up to 180 degrees.
We have angles A and B. We can calculate angle C as follows;
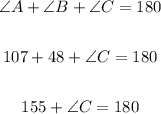
Subtract 155 from both sides;
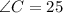
Therefore, the angles are;
ANSWER: