Question

What is the equation in slope-intercept form of the line that passes through the points (5, -6) and (25, 10)?A.y = 0.8x - 10B.y = 1.25x + 12C.y = 1.25x - 10D.y = 0.8x + 3+

Answer 1

We are asked to find the equation of the line in slope-intercept form that passes through the following points.

`(5,-6)\text{ and }(25,10)`

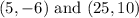
Recall that the equation of the line in slope-intercept form is given by

`y=mx+b`

Where m is the slope and b is the y-intercept.

The slope of the line is given by

`m=(y_2-y_1)/(x_2-x_1)`
`\text{Where (}x_1,y_1)=(5,-6)\text{ and (}x_2,y_2)=(25,10)`

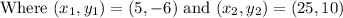
Let us substitute the given values into the slope formula

`m=(10-(-6))/(25-5)=(10+6)/(20)=(16)/(20)=(4)/(5)=0.8`

So the equation of line at this point is

`y=0.8x+b`

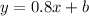
Now let us find the y-intercept (b)

Choose any one point from the given two points

Let choose (5, -6) and substitute it into the above equation

`\begin{gathered} -6=0.8(5)+b \\ -6=4+b \\ b=-6-4 \\ b=-10 \end{gathered}`

Therefore, now we got both slope and y-intercept

So the equation of the line in slope-intercept form is

`y=0.8x-10`

Option (A) is correct.