Answer:
(14, -8)
Explanation:
Given the function:
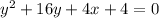
We want to find the coordinates of the focus of the parabola.
A parabola is the locus of points such that the distance to the focus equals the distance to the directrix. For a right-left facing parabola with vertex at (h, k), and a focal length |p|, the standard equation is:
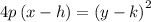
First, we rewrite the given equation in the standard equation form:
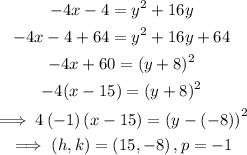
Next, our parabola is symmetric around the x-axis and so the focus lies at a distance p from the center (15,-8) along the x-axis. Thus, the coordinates of the focus is:
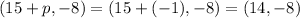
The focus is at (14, -8).