Question

A woman can bicycle 52 miles in the same time as it takes her to walk 16 miles. She can ride 9 mph faster than she can walk. How fast can she walk?_______mph

Answer 1

4 mph

Step-by-step explanation

Step 1

let x represents the speed when she bicycle

let y represents the speed when she walks

so,

A woman can bicycle 52 miles in the same time as it takes her to walk 16 miles.

`\begin{gathered} \text{time}=\frac{dis\tan ce}{\text{sped}} \\ time_b=time_w \\ (52)/(x)=(16)/(y) \\ \text{cross multiply} \\ 52\cdot y=16\cdot x \\ 52y=16x\rightarrow equation\text{ (1)} \end{gathered}`

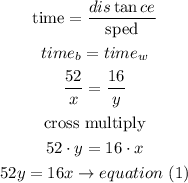
and

She can ride 9 mph faster than she can walk, ( in other words you have to add 9 to the spee when she walks to obtain the speed when she runs,

`x=y+9\rightarrow equation\text{ (2)}`

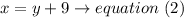
Step 2

solve for y

`\begin{gathered} 52y=16x\rightarrow equation\text{ (1)} \\ x=y+9\rightarrow equation\text{ (2)} \end{gathered}`

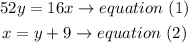
replace the x value from equation (2) in equation (1).

`\begin{gathered} 52y=16x\rightarrow equation\text{ (1)} \\ 52y=16(y+9) \\ 52y=16y+144 \\ \text{subtract 16 y in both sides} \\ 52y-16y=16y+144-16y \\ 36y=144 \\ \text{divide both sides by 36} \\ (36y)/(36)=(144)/(36) \\ y=4 \end{gathered}`

so, she can walk to 4 miles per hour

I hope this helps you