Question

Find the derivatives of the following using increment method.1. y= 3x² - 2x + 52.y = 6x² +10x - 3

Answer 1

y'=6x-2

Explanation:

Given the function:

`y=3x^2-2x+5`

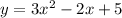
We want to find the derivative using the increment method.

First, replace y with y+△y and x with x+△x.

`\begin{gathered} y+\Delta y=3(x+\Delta x)^2-2(x+\Delta x)+5 \\ \text{Make }\Delta y\text{ the subject of the equation} \\ \Delta y=3(x+\Delta x)^2-2(x+\Delta x)+5-y \\ \text{ Replace y with the initial function given} \\ \Delta y=3(x+\Delta x)^2-2(x+\Delta x)+5-(3x^2-2x+5) \end{gathered}`

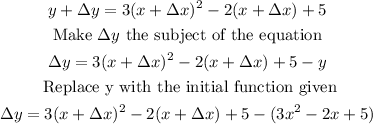
Next, simplify the right-side of the equation:

`\begin{gathered} \Delta y=3(x^2+2x\Delta x+(\Delta x)^2)-2x-2\Delta x+5-3x^2+2x-5 \\ \Delta y=3x^2+6x\Delta x+3(\Delta x)^2-2x-2\Delta x+5-3x^2+2x-5 \\ \Delta y=3x^2-3x^2+6x\Delta x+3(\Delta x)^2-2x+2x-2\Delta x+5-5 \\ \Delta y=6x\Delta x+3(\Delta x)^2-2\Delta x \end{gathered}`

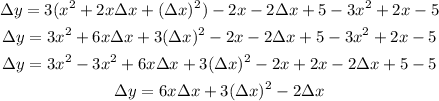
Factor out △x in the right-side of the equation:

`\Delta y=\Delta x(6x+3(\Delta x)-2)`

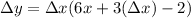
Divide both sides by △x:

`\begin{gathered} (\Delta y)/(\Delta x)=(\Delta x(6x+3\Delta x-2))/(\Delta x) \\ (\Delta y)/(\Delta x)=6x-2+3\Delta x \end{gathered}`

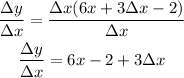
Let △x tends to 0:

`(\Delta y)/(\Delta x)=6x-2`

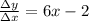
The derivative of y is 6x-2.