Since the value of the care dropped by 15% each year, then we can represent this situation by a geometric sequence with a common ratio of 100% - 15% = 85%
Change the percentage to a decimal by dividing it by 100
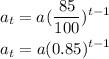
a is the initial value of the car
t is the number of years
b.
Since the initial value is $15000
Then a = 15000
The explicit formula is
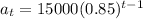
c.
If t = 5
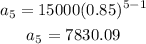
Then the price of the care after 5 years will be $7830.09 to the nearest cents
The value on the table is $12750
Then they are not the same
d.
If t = 7, then
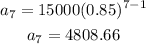
Then the value of the car after 7 years is $4808.66 to the nearest cent