Question

Express the trig ratios as fractions in simplest terms.J1617IV33sin J =cos K =are equalare not equalsin J and cos K

Answer 1

To answer this question, we always need to know what the reference angle is, and then we have to find the adjacent side and the opposite side to the angle. Since we have a right triangle here, we know that the largest side of the triangle is the hypotenuse. In this case, the value of the hypotenuse is equal to 17.

We can draw the angle J and angle K as follows:

Finding sin J

If we have the angle J, we can see that:

• The opposite side to angle J is the one in front of it, and it is the side KL = √33.

,

• The adjacent side is JL = 16.

Therefore, since we know that the sine ratio is given by:

`\sin (\theta)=(opp)/(hyp)`

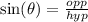
That is, the sine ratio (in a right triangle) is the ratio between the measure of the opposite side to the measure of the hypotenuse, then we have:

`\sin (J)=\frac{\sqrt[]{33}}{17}`

Since the factors for 33 are 3 and 11, we cannot simplify the radicand value. We also have that 17 is a prime number, and we cannot simplify it either.

Finding cos K

If we have that the reference angle is angle K, we have that:

• The opposite side is JL = 16

,

• The adjacent side is KL = √33

Since we have that the cosine ratio is:

`\cos (\theta)=(adj)/(hyp)`

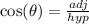
Then we have:

`\cos (K)=\frac{\sqrt[]{33}}{17}`

Therefore, since:

`\begin{gathered} \sin (J)=\frac{\sqrt[]{33}}{17} \\ \cos (K)=\frac{\sqrt[]{33}}{17} \\ \Rightarrow\sin (J)=\sin (K) \end{gathered}`

In summary, we have that:

`\sin J=\frac{\sqrt[]{33}}{17}`
`\cos K=\frac{\sqrt[]{33}}{17}`

And sin(J) and cos(K) are equal.