From Pythagoras's theorem the distance d between any two points on a graph is
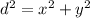
where x is the vertical distance and y is the horizontal distance.
Now, our points lie on the complex plane, but the Pythagoras's theorem still works because it is a fundamental theorem of geometry which works in every situation.
The vertical distance between the two points is

Remember that on the complex plane the imaginary numbers lie on the vertical axis.
The horizontal distance is
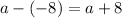
Now from the Pythagoras's theorem, the distance d between the two points is d
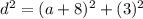
But we are told that this distance d is √130; therefore, we have
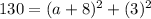

Now we just need to solve for a. To do this, we subtract 9 from both sides of the equation and then take the square root of both sides to get:
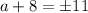
which gives us
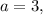

Since the desired value of a is a positive number, our answer is a = 3.