Question

the equation shows the radius of the algae,f(d), in mm,after d days: f(d)=7(1.06)^d the radius of the algae was approximately 13.29 mm, what is a reasonable domain to plot the growth function?

Answer 1

`\begin{gathered} A)\text{ }Domain:\text{ \lparen0,11\rparen} \\ B)\text{ the y-intercept represents that in 0 days the diameter of the algae will be 7 mm.} \\ C)\text{ rate of change= 0.64. This means that on average the algae grows 0.64mm per day.} \end{gathered}`

Explanation:

If the radius of the algae was approximately 13.29 mm, substitute f(d)=13.29 and solve for d to determine the domain:

`\begin{gathered} 13.29=7\left(1.06\right)^d \\ (13.29)/(7)=1.06^d \\ d=\frac{\text{ log\lparen13.29/7\rparen}}{\text{ log\lparen1.06\rparen}} \\ d=11 \\ \text{ Then, the domain:} \\ (0,11) \end{gathered}`

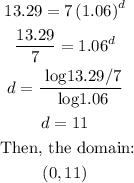
B. The y-intercept is obtained when d=0, hence;

`\begin{gathered} d=0 \\ f(0)=7(1.06)^0 \\ f(0)=7 \end{gathered}`

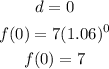
Therefore, the y-intercept represents that in 0 days the diameter of the algae will be 7 mm.

C. Now, to determine the rate of change of a function, use the following equation:

`\text{ rate of change=}\frac{change\text{ over y}}{change\text{ over x}}`

Then, determine the value of f(4):

`\begin{gathered} f(4)=7(1.06)^4 \\ f(4)=8.83 \end{gathered}`

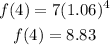
Hence, the rate of change on that interval of the function:

`\begin{gathered} \text{ rate of change=}(13.29-8.83)/(11-4) \\ \text{ rate of change=0.64 } \end{gathered}`

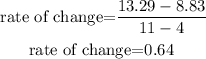
This means that on average the algae grows 0.64mm per day.