Question

What is the polar form of the equation?
`(x + 2) ^(2) + y ^(2) = 4`

Answer 1

`r(r+4\cos \theta)=0`

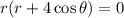
Step-by-step explanation

We want to convert the given equation to polar form:

`(x+2)^2+y^2=4`

The first step is to expand the bracket:

`\begin{gathered} (x+2)(x+2)+y^2=4 \\ x^2+2x+2x+4+y^2=4 \\ x^2+4x+y^2=4-4 \\ x^2+4x+y^2=0 \end{gathered}`

Now, we will convert it by carrying out the following transformations:

`\begin{gathered} x=r\cos \theta \\ y=r\sin \theta \\ x^2+y^2=r^2 \end{gathered}`

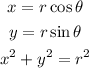
The equation then becomes:

`\begin{gathered} x^2+4(r\cos \theta)+y^2=0 \\ \Rightarrow x^2+y^2+4r\cos \theta=0 \end{gathered}`

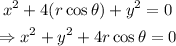
Therefore, it becomes:

`\begin{gathered} r^2+4\cos \theta=0 \\ \Rightarrow r(r+4\cos \theta)=0 \end{gathered}`

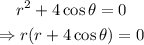
That is the polar form of the equation.