The given expression is
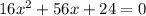
To determine the dimensions of the length and the height, we have to factor the expression.
We know that a = 16, b = 56, and c = 24. Remember that a is the coefficient of the quadratic variable, b is the coefficient of the linear variable, and c is the independent term.
Now, we use the quadratic formula
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/li72dimqx1poek8bdg3bs589861h83kfxl.png)
Let's replace all the values
![\begin{gathered} x_(1,2)=\frac{-56\pm\sqrt[]{56^2-4\cdot16\cdot24}}{2\cdot16} \\ x_(1,2)=\frac{-56\pm\sqrt[]{3136-1536}}{32}=\frac{-56\pm\sqrt[]{1600}}{32} \\ x_(1,2)=(-56\pm40)/(32) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tktcqxstfckeddu9msezgpba6nttih6e32.png)
We have two solutions here

If we express them as factors, it would be
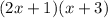
Which is equivalent to A.