A complex number z with modulus |z| and argument θ can be written as:
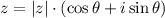
And the nth power of z can be written as:
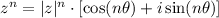
Thus, using the given hint, we have:
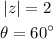
So, the fourth power of z is given by:
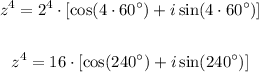
Now, notice that:
![\begin{gathered} \cos (240^(\circ))=-(1)/(2) \\ \\ \sin (240^(\circ))=-\frac{\sqrt[]{3}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/33q6xmb1yr7xqbw6zzr5y8ddrdzec3nv75.png)
So, we obtain:
![z^4=16\mleft(-(1)/(2)-\frac{\sqrt[]{3}}{2}i\mright)=-(16)/(2)-(16)/(2)\sqrt[]{3}i=-8-8\sqrt[]{3}i\cong-8-13.9i](https://img.qammunity.org/2023/formulas/mathematics/college/wlttx7yiudjkg818q3vpdk8dy7mmqaum2q.png)
Therefore, option D is correct.