Question

You inherited $5000 and decide to invest it into an account with an APR of 2.75% compounding quarterly. How much do you have in the account (i.e., the accumulated balance) after 10 years?

Answer 1

We know that

• The principal is $5000.

,

• The interest rate is 2.75%.

,

• The compound is quarterly.

,

• The time is 10 years.

We have to use the compound interest formula

`A=P(1+(r)/(n))^(nt)`

Where P = 5000, r = 0.0275, n = 4, and t = 10. Let's replace these values and solve for A.

`\begin{gathered} A=5000(1+(0.0275)/(4))^(4\cdot10) \\ A=5000(1+0.006875)^(40) \\ A=5000(1.32)=6,600 \end{gathered}`

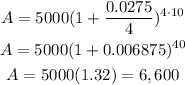
Hence, after 10 years, the accumulated balance would be $6,600, approximately.