Answer
From the figure of the tetrahedron above, the area of the cross section whose distance from the base is 15 is ΔDEF
/PB/ is the altitude of the tetrahedron = 20
/EB/ is the distance from cross section to the base of the tretrahedron = 15
⇒/PE/ = 20 - 15 = 5
Since 26² = 10² + 24², That is
676 = 100 + 576, ΔABC is a right triangle.
Since ΔDEF ≅ ΔABC, ΔDEF is also a right triangle.
ΔPED ≅ ΔPBA
To find /DE/;
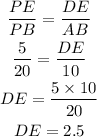
Since ΔPEF ≅ ΔPBC
Also, to find /EF/;
![undefined]()