Question

Write a system of equations to describe the situation belon, solve using substitution, and fill in the blanks.Two students in Mr. Sloan's class, Krysta and Rob, have been assigned a workbook to complete at their own pace. They get together at Krysta's house after school to complete as many pages as they can. Krysta has already completed 64 pages and will continue working at rate of 11 pages per hour. Rob has completed 66 pages and can work at a rate of 9 pages per hour. Eventually, the two students will be working on the same page. How many pages will each of them have completed? How long will that take?Krysta and Rob will each have completed ___ workbook pages in ___ hours.

Answer 1

The Slope-Intercept form of an equation of the line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

Let be "y" the number of pages they completed and "x" the number of hours.

You know that has completed 64 pages and will continue working at rate of 11 pages per hour. Then, you can write the following equation:

`y=11x+64`

Rob has completed 66 pages and work at a rate of 9 pages per hour. Then, you can set up this equation:

`y=9x+66`

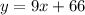
Then you get the following System of Linear equations:

`\begin{cases}y=11x+64 \\ y=9x+66\end{cases}`

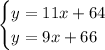
You can solve it using the Substitution method as following:

- Solve for "x" from the first equation:

`\begin{gathered} y-64=11x \\ \\ x=(y-64)/(11) \end{gathered}`

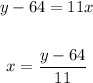
- Substitute it into the second equation and solve for "y":

`\begin{gathered} y=9((y-64)/(11))+66 \\ \\ y=(9y-576)/(11)+66 \\ \\ (11)(y-66)=9y-576 \\ 11y-726=9y-576 \\ 11y-9y=-576+726 \\ y=(150)/(2) \\ \\ y=75 \end{gathered}`

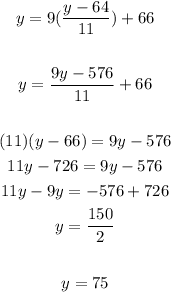
- Substitute the value of "y" into this equation:

`x=(y-64)/(11)`

Then:

`x=(75-64)/(11)`

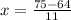
- Evaluating, you get:

`\begin{gathered} x=(11)/(11) \\ \\ x=1 \end{gathered}`

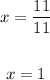
The answer is:

Krysta and Rob will each have completed 75 workbook pages in 1 hour.