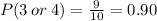Question

Find the probability that the number on the counter is 3 or 4

Answer 1

There are a total of 10 counters.

Count how many counters have the number 3 written on them.

There are 6 counters with the number 3 written on them.

The probability that the number on the counter is 3 is given by

`P(3)=(6)/(10)=(3)/(5)`

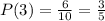
Now, count how many counters have the number 4 written on them.

There are 3 counters with the number 4 written on them.

The probability that the number on the counter is 4 is given by

`P(4)=(3)/(10)`

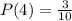
Finally, the overall probability is (or means to add the probabilities)

`P(3\: or\: 4)=(3)/(5)+(3)/(10)=(2\cdot3+3)/(10)=(6+3)/(10)=(9)/(10)`

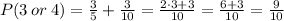
Therefore, the probability that the number on the counter is 3 or 4 is 9/10

`P(3\: or\: 4)=(9)/(10)=0.90`