Question

Ten pounds of mixed birdseed sells for $6.30 per pound. The mixture is obtained from two kinds of birdseed, with one variety priced at $5.66 per pound and the other at $8.86 per

pound. How many pounds of each variety of birdseed are used in the mixture?
$5.66/lb variety
lb
lb
$8.86/lb variety

Answer 1

$5.66lb variety : 8 lbs used

$8.86 variety: 2 lbs used

Explanation:

Let x be the lbs of $5.66 variety

Let y be the lbs of $8.86 variety

Total weight = x + y lbs

Total cost = 5.66 + 8.86y

The final mixture weighs x + y pounds and costs a total of 5.66x + 8.86y

So the cost per pound of the final mixture:

Total Cost/Total Weight

`( 5.66x + 8.86y)/(x + y)`

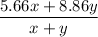
We are given that the final selling rate is $6.30

We are also given that the total weight is 10 lbs; so

`x + y = 10\dots[1]`

So we get

`( 5.66x + 8.86y)/(x + y) = 6.30\\\\`

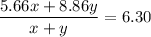
`\longrightarrow ( 5.66x + 8.86y)/(10) = 6.30\\\\\longrightarrow 5.66x + 8.86y = 10 * 6.30\\\\\\\longrightarrow 5.66x + 8.86y = 63\dots[2]\\\\`

Let's re-write equations [1] and [2] below and solve for them

`x + y = 10\dots[1]`

`5.66x + 8.86y = 63\dots[2]\\\\`

Eliminate one of the variable terms by making their coefficients equal

Multiply equation [1] by 8.86 to make the y terms equal

[1] x 8.86

`\longrightarrow 8,86x + 8.86y = 8.86 * 10\\\\\longrightarrow 8,86x + 8.86y = 88.6 \dots [3]`

Subtract equation [2] from equation [3]:

`8,86x + 8.86y = 88.6 \\-\\5.66x + 8.86y = 63.0\\\\----------\\3.20x \;\;\;\;\ + 0y= 25.6\\ \\`

`3.20x = 25.6\\`

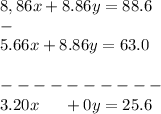
Divide both sides by 3.20 to get

`x = (25.6)/(3.20) = 8\\\\\text{From equation [1] we get:}x + y = 10\\8 + y = 10\\y = 2\\`

Answer:
$5.66lb variety : 8 lbs used

$8.86 variety: 2 lbs used