The first step to answer this question is to convert the given gallons to liters and then to mililites using the given conversion factors:
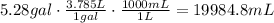
The second step is to convert the volume of water to mass using its given density:
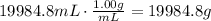
Finally, use the following formula to find the heat needed to raise the temperature of water:

Where Q is the heat, Cp is the specific heat, m is the mass and ΔT is the difference of temperatures. Replace for the given values and find Q:
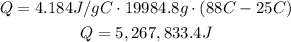
It means that the heat needed to raise the temperature of water is 5267833.4J.