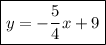Question

Write an equation passing through the points (-4,14) and (8,-1)

Answer 1

`\displaystyle {y = -(5)/(4)x+9}`

Explanation:

Givens

We are given two points of a line and asked to find the equation that goes through these points. These are given in the form:

`(x_1, y_1), (x_2, y_2)`

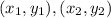
To do so, we will first determine the slope of the line using the formula for slope:

`\displaystyle m = (y_2-y_1)/(x_2-x_1)`

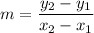
Then, we will use the point-slope formula to find the equation of the line in slope-intercept form.

Point-Slope Formula

`y-y_1=m(x-x_1)`

Slope-Intercept Form

`y=mx+b`

Solve

First, use the slope formula to find the slope of the equation:

`\displaystyle m = (y_2-y_1)/(x_2-x_1)\\\\\\\displaystyle m = (-1-14)/(8-(-4))\\\\\\\displaystyle m = (-15)/(12) = -(15)/(12)\\\\\\\displaystyle m = -(5)/(4)`

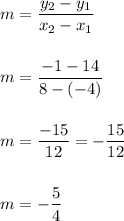
Then, use the point-slope formula to substitute values and find the equation of the line in slope-intercept form:

`y-y_1=m(x-x_1)\\\\\\\displaystyle y-14=-(5)/(4)(x-(-4))\\\\\\\displaystyle y-14=-(5)/(4)x-5\\\\\\\displaystyle y-14+14=-(5)/(4)x-5+14\\\\\\\displaystyle{y = -(5)/(4)x+9}`

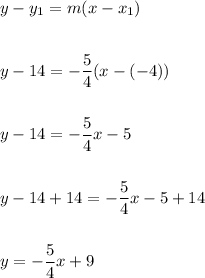
Final Answer

The equation of a line passing through the points (-4, 14) and (8, -1) is:

`\displaystyle \boxed{y = -(5)/(4)x+9}`