Question

LOOK AT THE IMAGE ATTACHED! :)

Answer 1

`\bold {\boxed {y = -4x^2 +24x - 28}}`

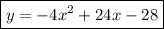
Explanation:

A quadratic equation is of the form

`\displaysize {y = ax^2 + bx + c}\\\\`

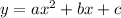
This can be written in the vertex form as

`y = (x-h)^2 + k\\\\`

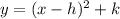
where (h, k) are the coordinates of the vertex of the quadratic parabola

Since

`f(3 + \sqrt2) = 0 \\f(3 - \sqrt2) = 0\\\\`

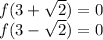
The roots of the equation from the given data are

`x = 3 + \sqrt2 \;and \\\\x = 3 - \sqrt2\\\\`

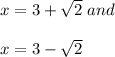
This means the axis of symmetry is at x = 3 or h = 3

The equation in vertex form is therefore

`y = a(x -3)^2 + k`

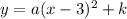
Since

`f(3 + \sqrt2) = 0`

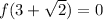
Substituting for
`x = 3 + \sqrt2 \textrm{ in the vertex equation above gives us}`

`y = a(3 + \sqrt2 - 3)^2 + k = 0\\\\`

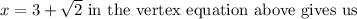
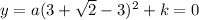
`\rightarrow a(\sqrt2)^2 + k = 0\\\\\\\rightarrow 2a + k = 0\\\\`[1]

We are also given y = -8 when x = 1

Therefore substituting for x = 1 we should get

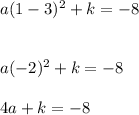`a(1-3)^2 + k = -8\\\\\\a(-2)^2 + k = -8\\\\4a + k = -8\\\\`[2]

Subtract Equation [1] from equation [2] to eliminate k and get

4a - 2a = - 8 -0

2a = -8

a = -4

Substitute for a in equation2a + k = 0 to get

2(-4) + k = 0

-8 + k = 0

k = 8

Therefore the equation in vertex form is

y = -4(x-3)² + 8

We can rewrite this in the standard form as

==> -4(x² - 6x + 9) + 8

==> -4x² + (-4)(-6)x +(-4)(9) + 8

==> -4x² +24x -36 + 8

==> -4x² + 24x - 28

So the quadratic equation is

`\bold {\boxed {y = -4x^2 +24x - 28}}`

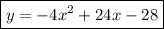
The attached plot shows the parabola with all the parameters

Since the coefficient of x², a, is negative, the parabola opens downward