Question

Find twe positive even consecutive intecers such

that the square of the smaller integer is 10 more
than the larger integer.

Answer 1

4 and 6

Explanation:

x = smaller integer

x+2 = larger integer

x² = 10 + (x + 2)

x² = x + 12

x² - x - 12 = 0

factors are:

(x-4)(x+3) = 0

x-4=0; x = 4

x+3=0; x = -3

Since the question states the numbers are even and positive we use only the 4 and the next consecutive even integer is 6

Answer 2

The numbers are 4 and 6

Explanation:

Let:

• x - the smaller even consecutive integer
• x+2 - the larger even consecutive integer

we know that

`x^(2) =(x+2)+10`

solve for x

`x^(2) -x-12=0`

We can use the quadratic formula for quadratics in the form
`ax^(2) +bx+c=0`

`x= \frac{-b(+/-)\sqrt{b^(2) -4ac}}{2a}`

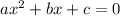
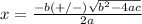
to give us an answer of 4 and -3

Since the question states positive and even we use 4 and that gives us 6 as the other answer
4 and 6