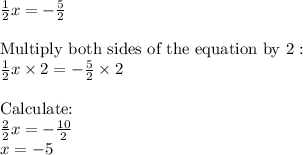Answer:
The solution to the equation is:

Explanation:
Step 1: Rearrange the equation
Since we have to solve the equation for
 , let's bring the
, let's bring the
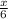 to the other side with all the other variables:
to the other side with all the other variables:
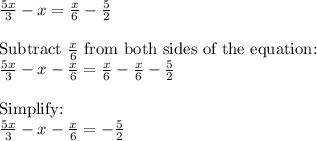
Step 2: Make use of the distributive property
The property states that when there's an expression like
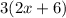 , it can be written as
, it can be written as
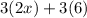 , or vice versa.
, or vice versa.
In the equation we have found above, the left hand side of the equation has a common variable:

Using the principle of distributive property, we can arrange the left hand side differently:
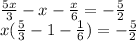
We have arranged the left hand side as such, that distributive property is applicable for it.
Step 3: Solving
First, let's simplify the equation:
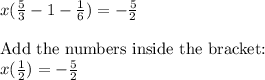
Now, let's solve it: