Answer:
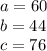
Explanation:
You can write these equations to represent the problem:
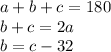
Now, just solve it as a system of equations. I'll solve by substitution, starting from the bottom as b is already defined there.
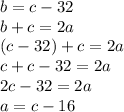
That's the middle equation done, now I'll do the top one:
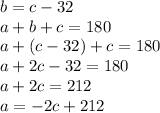
Now we have just 2 equations with 2 variables. That's another system of equations, but this one is much easier to solve. Using substitution again:
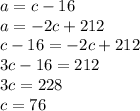
Finally, we have one variable solved. Using the value of C, now we can solve for A:
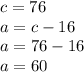
Thats 2 done. Now, pick any equation that has all 3 variables and solve for B:
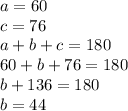
All 3 variables done.
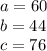
Now, we can confirm that they're correct by checking with the original equations:

They all work fine.