Question

In a pulley system, two blocks are connected by a rope as shown below. The coefficient of static friction between block A and the surface is 0.8. Block A has a mass of 20kg. What is the minimum mass that block B can have so that block A moves?

Answer 1

Hi there!

We can begin by doing a summation of forces for each block.

Block A:

This block has the force of tension (in direction of acceleration +) and static friction (opposite direction -) acting on it. Thus:


`\Sigma F_A = T - F_s\\\\m_Aa = T - \mu m_Ag`

Block B:

This block has the force of tension (opposite of acc. -) and gravity (in direction of acc +), working on it.

`\Sigma F_B = m_Bg - T\\\\ m_Ba = m_Bg - T`

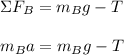
Add both of the expressions and solve for the maximum mass of Block B.

`\Sigma F = m_Bg - T + T - \mu m_Ag\\\\a(m_A + m_B) = m_Bg - \mu m_Ag`

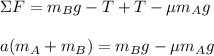
To find the minimum value, we can set a = 0, so:

`0 = m_Bg - \mu m_Ag\\\\\mu m_Ag = m_B g\\\\0.8(20)(9.8) = m_B (9.8)\\\\m_B = (0.8(20)(9.8))/(9.8)) = \boxed{16 kg}`

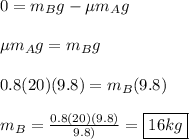
The block must weigh > 16 kg for block A to move.