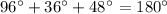Question

The ratio of the measures of the angles in atriangle is 8:3:4. Find the measures of theangles.

Answer 1

We want to know the measures of the angles of a triangle, given that the ratio of them is 8:3:4. Also, the sum of the angles must be 180°.

As their ratio is 8:3:4, we have that the angles of the triangles should be 8x, 3x and 4x (where x represents just a part of the división of the angles). Thus:

`8x+3x+4x=180^(\circ)`

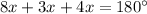
Solving for x, we obtain:

`\begin{gathered} 15x=180^(\circ) \\ x=(180^(\circ))/(15)=12^(\circ) \end{gathered}`

And thus, the angles will be:

`\begin{gathered} 8x=8(12^(\circ))=96^(\circ) \\ 3x=3(12^(\circ))=36^(\circ) \\ 4x=4(12^(\circ))=48^(\circ)_{} \end{gathered}`

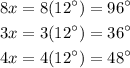
This means that the angles of the triangle should be: 96°, 36° and 48°. We verify that those are the angles of a triangle as:

`96^(\circ)+36^(\circ)+48^{\circ^{}}=180^(\circ)`