Answer for 1:
- Oxidation number of Mn in MnO4^-1= +7
- Oxidation number of O in MnO4^-1= -2
- Oxidation number of C in C2O4^-2= +3
- Oxidation number of O in C2O4^-2= -2
- Oxidation number of Mn in MnO2= +4
- Oxidation number of O in MnO2= -2
- Oxidation number of C in CO2= +4
- Balanced redox equation in basic solution:
![3C_2O_4^(-2)+2MnO_4^(-1)+4H_2O\operatorname{\rightarrow}6CO_2\text{ +}2MnO_2\text{ + }8OH^-]()
Explanation for 1:
1st) To determine the oxidation numbers, it is necessary that the total sum of the charges is equal to that of the molecule or ion in the equation.
• Oxidation numbers in MnO4-,:
We know that the oxidation number for oxygen is -2, then we multiply it by the subscript 4 to find the whole charge of oxygen in this molecule.
Oxygen oxidation number: -2 x 4 = -8
Since the total charge of the molecule is -1, by difference, we will know that the oxidation number of Mn will be +7:
![\begin{gathered} Mn^(+7)O_4^(-2) \\ +7+[(-2*4)]=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/kpha933fo7h1tzo1x98s9lyubglny1l247.png)
To confirm that the oxidation number that we determined exists for that element, we can check the Periodic Table of Elements.
We proceed in the same way with all molecules.
• Oxidation numbers in C2O4-2,:
![\begin{gathered} C_2^(+3)O_4^(-2) \\ (+3*2)+[(-2)*4]= \\ +6-8=-2 \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/ogdqbqzr2eiu4g89uh4ik6malodrcw6c0t.png)
• Oxidation numbers in MnO2,:
![\begin{gathered} Mn^(+4)O_2^(-2) \\ +4+[(-2)*2]= \\ +4-4=0 \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/6trqva2l2b12m7p4c97v8mi0lzkz31k4jo.png)
• Oxidation numbers in CO2,:
![\begin{gathered} C^(+4)O_2^(-2)_ \\ +4+[(-2)*2]= \\ +4-4=0 \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/nupkytpzsaha0pm1455gmqgs0cibn8ftrf.png)
2nd) Now that we know the oxidation number os each atom in the reaction, then we can find the element that is oxidized and the element that is reduced.
We can see that Mn goes from +7 to +4, the Mn atom is reduced. And, the carbon atom goes from +3 to +4 so it oxidizes.
3rd) It is necessary to write the oxidation reaction and the reduction reaction separately and balancing all elements except oxygen and hydrogen:
Oxidation:
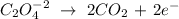
Reduction:
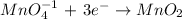
4th) Since the reaction occurs in a basic solution, we must add water (H2O) to balance the oxygen atoms and hydroxyl ion (OH-) to balance the hydrogen atoms. In this case, the reduction reaction is the only one that needs to be balanced with water and hydroxyl ion.
![MnO_4^(-1)\text{ + 3}e^-\text{ +2}H_2O\operatorname{\rightarrow}MnO_2\text{ + 4}OH^-]()
5th) It is necessary to balance the electrons in each half-reaction. So, we multiply each half-reaction by the number of electrons in the other half-reaction:
Oxidation:
![\begin{gathered} (C_2O_4^(-2)\operatorname{\rightarrow}\text{2}CO_2\text{ + 2}e_^-)*3 \\ 3C_2O_4^(-2)\operatorname{\rightarrow}6CO_2\text{ + 6}e^- \end{gathered}]()
Reduction:
![\begin{gathered} (MnO_4^(-1)\text{ + 3}e^-\text{ + 2}H_2O\operatorname{\rightarrow}\text{ MnO}_2\text{ }+4OH^-)*2 \\ 2MnO_4^(-1)\text{ + 6}e^-\text{ + 4}H_2O\operatorname{\rightarrow}\text{ 2MnO}_2\text{ }+8OH^- \end{gathered}]()
6th) We need to cancel out everything that is repeated on opposite sides of the reactions, including the electrons.
Finally, we can write the balanced redox equation:
![3C_2O_4^(-2)+2MnO_4^(-1)+4H_2O\operatorname{\rightarrow}6CO_2\text{ +}2MnO_2\text{ + }8OH^-]()