The perimeter of a rectangle can be determined as the sum of twice its width and twice its length, following the formula:
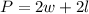
If you know the perimeter and length of a rectangle, you can determine its width using the formula.
The first step is to write the formula for w:
-pass 2l to the left side of the equal sign by applying the opposite operation to both sides of it:
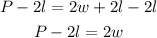
-divide both sides by 2
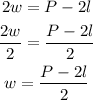
You know that the rectangular garden has a perimeter of P=370ft, and its length is l=98ft, replace both values on the formula obtained for w:
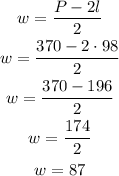
The width of the rectangular garden is 87ft