Given:
The graph of the f(x) is given.
Required:
To plot a line segment connecting the points on f where x=-2 and x=8 and to determine the average rate of change of the function f(x) on the interval −2≤x≤8.
Step-by-step explanation:
The line segment connecting the points on f where x=-2 and x=8 is,
The average rate of change = slope
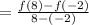
From the graph,
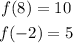
Therefore,
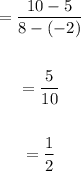
Final Answer:
Average rate of change is 1/2.