Solution:
Given that;
Luke has blue and red balls.
And, every day, he wins 2 blue balls and loses 3 red ones.
Let a represent the blue balls and b represent the read balls
After 5 days, he has the same amount of blue and red balls, i.e.
For 5 days, the number of blue balls won and red balls lost by Luke will be

After 5 days, he has the same amount of blue and red balls,
The number of blue and red balls will be
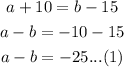
After 9 days, he has twice as many blue balls as red balls.
For 9 days, the number of blue balls won and red balls lost by Luke will be

After 9 days, he has twice as many blue balls as red balls.
The number of blue and red balls will be
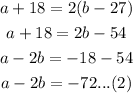
Solving the equation simltaneously, to find b (the number of red balls)
Appplying the elimonation method
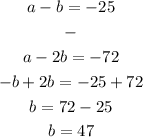
Hence, the number of red balls, b, at the beginning is 47