The range is the difference between the maximum and minimum value.
The maximum value is 4130 and the minimum is 2960. The range is then: 4130-2960=
A standard deviation of the sample is calculated with this formula:
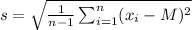
where n is the sample size, xi is each of the values of the sample and M is the mean of the sample.
First, we have to calculate the mean.
This is done as:
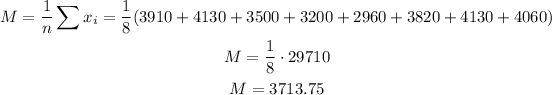
Now, we can start calculating the standard deviation.