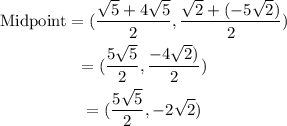Answer:
(a)3√13 Units
(b)
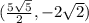
Step-by-step explanation:
Part A
We determine the distance between the two points using the distance formula.

Therefore, the distance between points (√5, √2) and (4√5, -5√2) is:
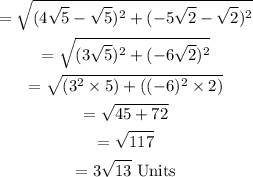
The exact distance between the points is 3√13 Units.
Part B
We determine the midpoint of the line segment whose endpoints are the given points using the midpoint formula.
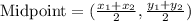
Therefore: