Answer:
• x=-6
,
• Not Reasonable, Length cannot be negative
Explanation:
In the given figure, the two triangles (ABC and DCE) are similar.
The ratio of corresponding sides is:
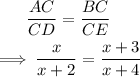
We solve for x:
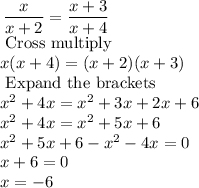
The value of x is -6.
Since x is a negative number, the dimensions are not reasonable as length cannot be negative.