Question

I need help. use the graph to answer the 3 questions pls

Answer 1

1. As the graph is exponential the sequence is geometric.

2. - Find the ratio r betwen each k(x) value and the previous one:

`\begin{gathered} (27)/(81)=(1)/(3) \\ \\ (9)/(27)=(1)/(3) \\ \\ (3)/(9)=(1)/(3) \\ \\ (1)/(3)=(1)/(3) \end{gathered}`

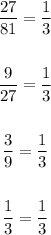
Use the next formula to get the recursive formula:

`\begin{gathered} k_1=\text{first term} \\ k(x)=r\cdot k_(x-1) \end{gathered}`

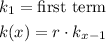
Being k1 the first term (81)

r the ratio you find above: (1/3)

k(x-1) is the prevoius term

You get the next recursive formula:
`\begin{gathered} k_1=81 \\ k(x)=(1)/(3)k_(x-1) \end{gathered}`

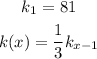
3. As x is the number of cuts, it cannot be a negative number. And it needs to be an inerger number (as the number of cuts cannot be a decimal number)

Then:

`x\ge0;x\in Z`

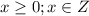
x can be any interger possitive number (example: 6,7,8) also, the number of cuts cannot be a very large number as you cannot cut an object in infinitely parts.

Then, x can be a possitive interger and cannot be a negative number, a decimal, or a very large possitive interger