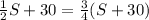Question

James and his sister save money for a trip to the water park.James have saved half the amount of money that his sister has saved. if they both save 30$ more, James will have saved 3/4 as much as his sister. Which equation can you use to find how much has saved A. 1/2+30=3/4x+30B. 1/2(x+30)=3/4(x+30)C. 1/2x+30=x+30D. 1/2x+30=3/4(x+30)

Answer 1

Let J be the money that James saved and let S be the money of his sister.

We have that JAmes saved half the money that his sister saved, then:

`J=(1)/(2)S`

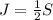
then if they both save $30, then james will have saved 3/4 as much as his sister. To represent this in the equation, we have to add 30 to the previous eqution (since James saved $30):

`J=(1)/(2)S+30`

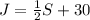
But with the $30 more, James will have 3/4 as much as his sister:

`J=(3)/(4)(S+30)`

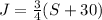
Now, if we match both equations we get:

`(1)/(2)S+30=(3)/(4)(S+30)`