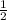Question

Use the sum and difference identities to determine the exact value of the following expression. If the answer is undefined, write DNE.esin 115 cos35 + cos1 15 sin35

Answer 1

Given the following expression;

`\sin 115\cos 35+\cos 115\sin 35`

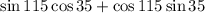
We begin by using the following trig identity;

`\cos A\sin B+\cos B\sin A=\sin (A+B)`

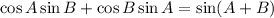
Using the values of the angles given, we have;

`\begin{gathered} \sin 115\cos 35+\cos 115\sin 35=\sin (115+35) \\ =\sin 150 \end{gathered}`

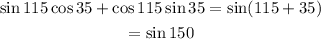
We can now rewrite as follows;

`\sin 150=\sin (60+90)`

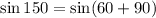
We can now apply the summation identity as identified earlier and we'll have;

`\sin (60+90)=\sin 60\cos 90+\cos 60\sin 90`

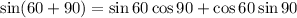
At this point we can apply the values of special angles, as shown;

`\begin{gathered} \sin 60=\frac{\sqrt[]{3}}{2},\cos 60=(1)/(2) \\ \sin 90=1,\cos 90=0 \end{gathered}`

Substitute these and we now have;

`\begin{gathered} \sin (60+90)=(\frac{\sqrt[]{3}}{2}*0)+((1)/(2)*1) \\ \sin (60+90)=0+(1)/(2) \\ \sin (60+90)=(1)/(2) \end{gathered}`

ANSWER;

The exact value of the given expression is

`(1)/(2)`