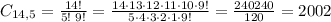Question

There are eight black balls and six red balls in an urnIf 5 balls are drawn without replacement what is the probability that exactly one blackball is drawn express your answer as a fraction or decimal number rounded to four decimal places

Answer 1

There are 8 black balls and 6 red balls in an urn.

Five out of the total of 14 balls are to be taken out of the urn without replacement.

It's required to find the probability that only one of the balls is black. The other 4 balls will obviously be red.

The black ball will come randomly from the 8 black balls, so the possible ways to do so are:

`C_(8,1)=\frac{8!}{1!\text{ }7!}=(8\cdot7!)/(1\cdot7!)=8`

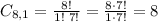
The 4 red balls are chosen from the 6 available, so the possible ways to do so are:

`C_(6,4)=\frac{6!}{4!\text{ }2!}=\frac{6\cdot5\cdot4!}{4!\text{ }2\cdot1}=(30)/(2)=15`

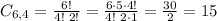
The total possible forms to extract the 5 balls are:

`C_(14,5)=\frac{14!}{5!\text{ 9}!}=(14\cdot13\cdot12\cdot11\cdot10\cdot9!)/(5\cdot4\cdot3\cdot2\cdot1\cdot9!)=(240240)/(120)=2002`