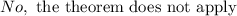1 Answer

Fadeproof · Answer 1 · 2023-09-09T20:57:25+0000

Step 1

There are two criteria for the Mean Value Theorem to be valid.

1) The function must be continuous on the interval and

2) the function must be differentiable on the interval.

Step 2

So for criterion 1) Is the function continuous on [1,5]

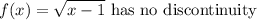
$\begin{gathered} f(x)=√(x-1)\text{ has no discontinuity} \\ \end{gathered}$

For criterion 2) is the function differentiable on the interval?

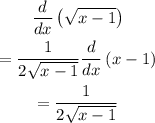
$\begin{gathered} (d)/(dx)\left(√(x-1)\right) \\ =(1)/(2√(x-1))(d)/(dx)\left(x-1\right) \\ =(1)/(2√(x-1)) \end{gathered}$

At the interval [1,5]

$\begin{gathered} f(1)=(1)/(2(√(1-1)))=(1)/(0)=undefined \\ f(5)=(1)/(2√(5-1))=(1)/(4) \\ \end{gathered}$

Since the function is not differentiable over the interval x=1, This means the conditions are not met and the answer will;

$No,\text{ the theorem does not apply}$

Please log in or register to add a comment.