Answer: We essentially have to find the variable L, provided the value of the duration of one complete swing, or the period:
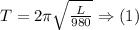
The value of the variable T is a known quantity in the equation (1), therefore plugging it into the equation (1) gives the following equation:
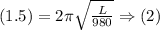
The solution is found by solving for the variable L in the equation (2), the steps for the answer are as follows:
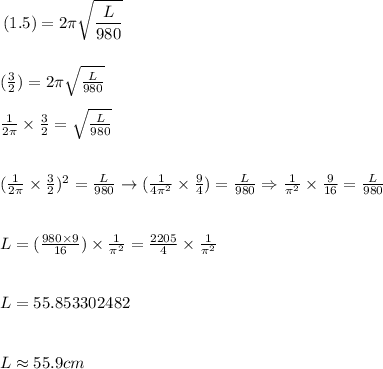
The answer is 55.9 centimeters or Option C.