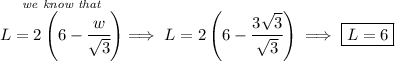Question

Using derivatives+optimization, find the dimensions of the rectangle of largest area that can be inscribed in an equilateral triangle of side 12.

Answer 1

Check the picture below atop.

we know is an equilateral triangle, meaning that all its interior angles are 60°, and thus if we run a line from the top vertex as you see there, we end up with a 30-60-90 triangle, either way there's an equation to get its height, and anyhow the altitude of it is 6√3.

As the rectangle moves up and down the triangle, with the rectangle having a width of "w" and a length of "L", the triangle that it forms above itself is a triangle, always with a base of "L" and a height of 6√3 - w.

BTW we laid the rectangle as you see on the bottom side, but laying it anywhere else it'd have ended up in the same arrangement.

well, with the bottom of the rectangle beign parallel to that of the side of the circumscribing triangle, the small upper triangle is similar to the containing triangle by AAA, and since we have similar triangles, we can say that.

`\cfrac{6√(3)}{12}=\cfrac{6√(3)-w}{L}\implies \cfrac{√(3)}{2}=\cfrac{6√(3)-w}{L}\implies L√(3)=12√(3)-2w \\\\\\ L=\cfrac{12√(3)-2w}{√(3)}\implies L=12-\cfrac{2w}{√(3)}\implies L=2\left(6-\cfrac{w}{√(3)} \right) \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{Area of the rectangle}}{A=wL\implies A(w)=w\cdot 2\left(6-\cfrac{w}{√(3)} \right)}\implies A(w)=2\left(6w-\cfrac{w^2}{√(3)} \right)`

`\cfrac{dA}{dw}=2\left(6-\cfrac{2w}{√(3)} \right)\implies \cfrac{dA}{dw}=4\left(3-\cfrac{w}{√(3)} \right) \\\\[-0.35em] ~\dotfill\\\\ 0=4\left(3-\cfrac{w}{√(3)} \right)\implies \boxed{w=3√(3)}`

hmmm the way I usually run a 1st derivative test is, by using the critical point and slicing from it just a tiny bit, like say 3√3 - 0.000000001 to check the region on the left and then 3√3 + 0.000000001 to check the region on the right.

Check the picture at the bottom, the 1st derivative test more or less gives us those values, positive on the left-side and negative on the right-side, meaning as you can see in the arrows, is a maximum at that point.

`\stackrel{\textit{we know that}}{L=2\left(6-\cfrac{w}{√(3)} \right)}\implies L=2\left(6-\cfrac{3√(3)}{√(3)} \right)\implies \boxed{L=6}`