Question

How to find the equation for this quadratic when I'm only allowed to use the coordinates (1.7,0.059) (2.5,0.201) (1.073, 0.276) and can't use the x or y intercept.

Answer 1

Explanation:

Given three points on the graph of a quadratic equation:

`\begin{gathered} (1.7,0.059) \\ (2.5,0.201) \\ \mleft(1.073,0.276\mright) \end{gathered}`

Substitute these values into the standard form of a quadratic equation:

`y=ax^2+bx+c`

This gives rise to the system of equations:

`\begin{gathered} (1.7,0.059)\implies2.89a+1.7b+c=0.059\cdots(1) \\ (2.5,0.201)\implies6.25a+2.5b+c=0.201\cdots(2) \\ (1.073,0.276)\implies1.151329a+1.073b+c=0.276\cdots(3) \end{gathered}`

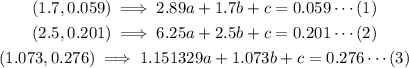
Using a calculator to solve the resulting system of equations, we have:

`\begin{gathered} a\approx0.366918 \\ b\approx-1.363557 \\ c\approx1.316653 \end{gathered}`

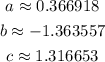
Note: The values of a, b and c are approximated correct to six decimal places.

Therefore, the equation for the quadratic graph is:

`y=0.366918x^2-1.363557x+1.316653`