Question

Hello, I need help with this last practice problem. Thank you!

Answer 1

Neither

Parallel

Neither

Parallel lines have the same slope while Perpendicular lines have slopes that are the negative reciprocals of each other.

Let us check the relation between lines 1 and 2:

`\begin{gathered} 6x+3y=12 \\ y=2x+1 \end{gathered}`

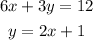
First, we rewrite and simplify line 1 into its slope-intercept form.

`\begin{gathered} 6x+3y=12 \\ \Rightarrow3y=-6x+12 \\ \Rightarrow y=-2x+4 \end{gathered}`

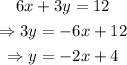
We now have the lines

`\begin{gathered} y=-2x+4 \\ y=2x+1 \end{gathered}`

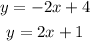
Since they do not have the same slope and the slopes are not the negative reciprocals of each other, Lines 1 and 2 are neither parallel nor perpendicular.

Next, in Lines 1 and 3, we have:

`\begin{gathered} y=-2x+4 \\ y=-2x-7 \end{gathered}`

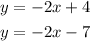
Since they have the same slope, these lines are parallel lines.

Lastly, we have lines 2 and 3. We have:

`\begin{gathered} y=2x+1 \\ y=-2x-7 \end{gathered}`

Just like lines 1 and 2, since they do not have the same solution and are not the negative reciprocal of each other, lines 2 and 3 are neither parallel nor perpendicular lines.