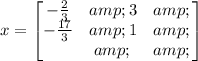Question

Problem 3: Find the matrix "X" that makes the equation true: 11 ЗХ. [? -13 15 -19 1 2

Answer 1

The matrix is given as :

`3\cdot x\text{ -}\begin{bmatrix}{11} & {-6} & {} \\ {2} & {1} & \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-13} & {15} & {} \\ {-19} & {2} & {} \\ {} & {} & {}\end{bmatrix}`

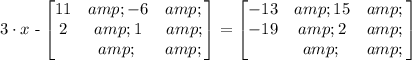
You should find matrix x that multiplies by 3 and subtracts the second matrix to get the answer matrix

Add the second matrix and the answer matrix and equate to 3x as;

`3x\text{ =}\begin{bmatrix}{11} & {-6} & {} \\ {2} & {1} & {} \\ {} & {} & \end{bmatrix}+\begin{bmatrix}{-13} & {15} & \\ {-19} & {2} & {} \\ {} & {} & {}\end{bmatrix}`

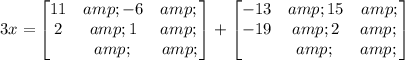
This will give;

`3x\text{ = }\begin{bmatrix}{11-13} & {-6+15} & {} \\ {2-19} & {1+2} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-2} & {9} & {} \\ {-17} & {3} & {} \\ {} & {} & {}\end{bmatrix}`

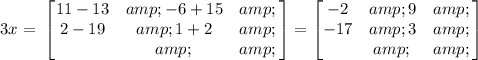
Divide every value in the answer matrix by 3 to get the x matrix as;

`x=\begin{bmatrix}{-(2)/(3)} & {(9)/(3)} & {} \\ {-(17)/(3)} & {(3)/(3)} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-(2)/(3)} & {3} & \\ {-(17)/(3)} & {1} & {} \\ {} & {} & {}\end{bmatrix}`

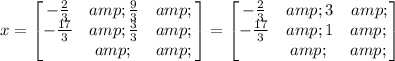
Answer is :

`x=\begin{bmatrix}{-(2)/(3)} & {3} & {} \\ {-(17)/(3)} & {1} & {} \\ {} & {} & {}\end{bmatrix}`