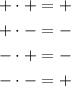Question

How do you Multiply fractions? could you explain with a few examples?

Answer 1

Multiplying fractions starts with the multiplication of the given numerators, followed by the multiplication of the denominators. ...

Example: Multiply the following fractions: 1/3 × 3/5.

Solution: We start by multiplying the numerators: 1 × 3 = 3, then, multiply the denominators: 3 × 5 = 15.

Answer 2

The first step when multiplying fractions is to multiply the two numerators. The second step is to multiply the two denominators. Finally, simplify the new fractions. For example

`\begin{gathered} (2)/(3)\cdot(5)/(6)=(2\cdot5)/(3\cdot6)=(10)/(18) \\ \text{ Now simplify} \\ (10)/(18)=(2\cdot5)/(2\cdot9)=(5)/(9) \\ \text{Then} \\ (2)/(3)\cdot(5)/(6)=(5)/(9) \end{gathered}`

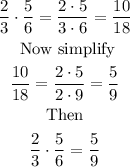
In other words, multiply linearly and simplify

If you have to multiply mixed fractions, first you transform the fraction from mixed to improper and then multiply, for example

`\begin{gathered} 3(1)/(4)\cdot-(8)/(5)=(3\cdot4+1)/(4)\cdot-(8)/(5)=(12+1)/(4)\cdot-(8)/(5)=(13)/(4)\cdot-(8)/(5) \\ \text{ Apply the law of signs of the multiplication} \\ 3(1)/(4)\cdot-(8)/(5)=(13)/(4)\cdot-(8)/(5)=(13\cdot-8)/(4\cdot5)=(-104)/(20) \\ \text{Simplify} \\ (-104)/(20)=(2\cdot-26)/(2\cdot10)=(-26)/(10) \\ \text{Then} \\ 3(1)/(4)\cdot-(8)/(5)=(-26)/(10) \end{gathered}`

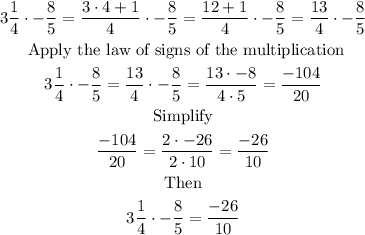
The law of signs for multiplication is

`\begin{gathered} +\cdot+=+ \\ +\cdot-=- \\ -\cdot+=- \\ -\cdot-=+ \end{gathered}`