We need to calculate the expression for f(x+h) before we can find the difference quotioent.
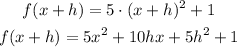
Now we can replace the value of f(x+h) and the value of f(x) on the expression, and simplify it as much as possible to determine the quotient.

The value of the quotient is "10x + 5h"