Given data:
* The mass of the CD is m = 15.8 g.
* The diameter of the CD is D = 12 cm.
* The tangential velocity of the CD is v =1.2 m/s.
* The music is detected at the radius of r = 29 mm.
Solution:
The moment of inertia of CD is,
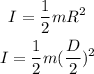
Substituting the known values,
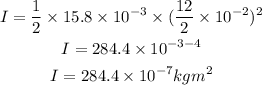
The initial kinetic energy of the CD is,
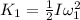
where,

As the CD is initially at rest, thus, the initial kinetic energy of the CD is,
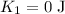
The final kinetic energy of the CD is,
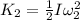
where,
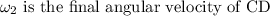
The angular velocity of the CD in terms of the translational velocity and radius of CD at which the music is detected,
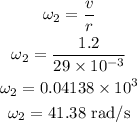
Thus, the final kinetic energy is,
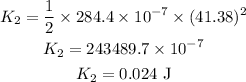
The work done on the CD is the change in its kinetic energy, thus, the work done is,
