Question

3. The Leakey Shipping Company uses small containers with a volume of 2.5 m3and large containers with a volume of 4 m3. A shipment of 140 containers hada total volume of 440 m3. Find the number of each size container used.

Answer 1

Given:

• Volume of small containers = 2.5 m³

,

• Volume of large containers = 4 m³

,

• Number of containers in the shipment = 140

,

• Total volume = 440 m³

Let's find the number of the size of each container used.

Let s represent the number of small containers

Let L represent the number of large containers.

• Equation for number of containers:

s + L = 140

• Equation for total volume:

2.5s + 4L = 140

Hence, we have the set of equations:

s + L = 140...........................equation 1

2.5s + 4L = 440...................equation 2

Let's solve the set of equations simultaneously using substitution methos.

Rewrite equation 1 for L:

L = 140 - s...........................equation 3

Substitute (140 -s) for L in equation 2:

2.5s + 4(140 - s) = 440

Apply distributive property:

2.5s + 4(140) + 4(-s) = 440

2.5s + 560 - 4s = 440

Combine like terms:

2.5s - 4s + 560 = 440

-1.5s + 560 = 440

Subtract 560 from both sides:

-1.5s + 560 - 560 = 440 - 560

-1.5s = -120

Divide both sides by -1.5:

`\begin{gathered} (-1.5s)/(-1.5)=(-120)/(-1.5) \\ \\ s=80 \end{gathered}`

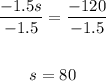
Substitute 80 for s in either of the equations.

Take equation 3.

L = 140 - s

L = 140 - 80

L = 60.

Therefore, we have the solutions:

s = 80 and L = 60

Therefore, the company used 80 small containers and 60 large containers