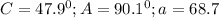Explanation
The first step is to recreate the triangle using the given values.
We can find the value of angle C using the sine rule below.
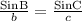
We insert the necessary parameters.
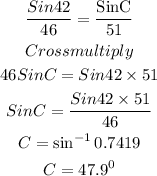
We can find the value of A using the sum of angles in a triangle.
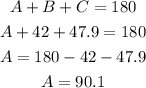
We can find the side "a" using the cosine rule
![\begin{gathered} a^2=b^2+c^2-2\text{bc}* CosA \\ a^2=46^2+51^2-2*46*51\text{Cos}90.1 \\ a^2=2116+2601+8.1891 \\ a^2=4725.1891 \\ a^{}=\sqrt[]{4725.1891} \\ a=68.7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ufxuo3paxhnxq9vg3iqx8sn0x8aflf6dhs.png)
Answer: