We will find the length arc, using the following formula
Therefore, to find the length of an arc we have to multiply the radius of the circle by the central angle in radians.
Let`s identify in this question, who is the radius and the central angle for the arc JM

Therefore, we can calculate:
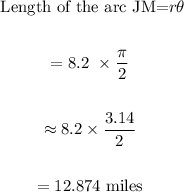
We conclude that the length of the arc JM is 12.874 miles.