Question

Suppose that 5% of the time Henry goes to the movies twice a month, 30% of the time he goes to the movies once a month, and 65 % of the time he doesn't go to themovies at all in a given month. What is the expectedvalue for the number of times Henry goes to the movies during a month?

Answer 1

Let X be the random variable representing the number of times that Henry goes to the movies.

Then, the given probability values can be understood as,

`\begin{gathered} P(X=2)=0.05 \\ P(X=1)=0.30 \\ P(X=0)=0.65 \end{gathered}`

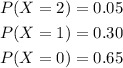
The expected value of X can be obtained by using the formula,

`E(X)=\sum ^{}_{}x\cdot P(X=x)`

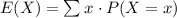
Substitute the values and simplify,

`\begin{gathered} E(X)=2\cdot(0.05)+1\cdot(0.30)+0\cdot(0.65) \\ E(X)=0.10+0.30+0 \\ E(X)=0.40 \end{gathered}`

Thus, the required expected value for the number of times that Henry goes to the movies in a month, is 0.40.