Question

Is the polynomial -x^3 a linear monomial? If not, how would -x^3 be classified as a polynomial?

Answer 1

It is not a linear monomial but a cubic monomial/polynomial

Explanation:

We have the following term:

`-x^3`

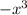
A polynomial is a "sum of monomials". Each of the addends that appear is called a term of the polynomial and each one is a monomial. The degree of the polynomial is the highest degree of the monomials that form it. Remember that monomials are special cases of polynomials.

In this case, the term is not a linear monomial since it is raising to the power of 3. Given the case that it is add another terms of the same degree or less, it would be a cubic polynomial.

Therefore, what we can say is that the expression is a cubic monomial/polynomial